Чему равна работа по растяжению пружины
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сила упругости — это сила, возникающая при упругой деформации тела и направленная в сторону, противоположную смещению частиц тела в процессе деформации. Силы, возникающие при пластических деформациях, не относятся к силам упругости.
Понятие о деформациях
Деформация — это изменение формы и размеров тела.
К деформациям относятся: растяжение, сжатие, кручение, сдвиг, изгиб.
Деформации бывают упругими и пластическими.
Закон Гука
Абсолютная величина силы упругости прямо пропорциональна величине деформации. В частности, для пружины, сжатой или растянутой на величину (displaystyle x) (разница между крайними положениями), сила упругости задается формулой [F=kx] где (displaystyle k) — коэффициент жесткости пружины.
Единицы измерения коэффициента жесткости: (k=)[Н/м].
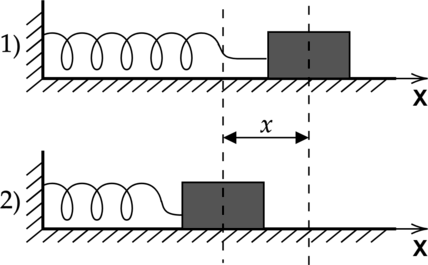
Закон Гука о линейной зависимости силы упругости от величины деформации справедлив лишь при малых деформациях тела.
Кубик массой (M = 2) кг, сжатый с боков пружинами, покоится на гладком горизонтальном столе. Первая пружина сжата на 2 см, а вторая сжата на 6 см. Жёсткость первой пружины (k_1 = 1200) Н/м. Чему равна жёсткость второй пружины (k_2)? Ответ выразите в Н/м.
По второму закону Ньютона силы упругости пружин будут уравновешивать друг друга, следовательно: [k_1Delta x_1=k_2Delta x_2] где (Delta x_1) и (Delta x_2) – сжатие первой и второй пружины соответственно.
Откуда жесткость второй пружины [k_2=dfrac{k_1 Delta x_1}{Delta x_2}= dfrac{1200text{ Н/м}cdot 2text{ см}}{6text{ см}}=400text{ Н/м}]
Ответ: 400
На штативе закреплён школьный динамометр. К нему подвесили груз массой 0,1 кг. Пружина динамометра при этом удлинилась на 2,5 см. Чему будет равно удлинение пружины, если масса груза увеличится втрое? (Ответ дайте в сантиметрах)
Согласно закону Гука [F=kDelta x] где k – жесткость пружины, ( Delta x) – удлинение пружины.
Найдем жесткость пружины, зная, что ( Delta x) = 2,5 см = 0,025 м при приложении силы, равно ( F=m_1g=0,1cdot 10=1text{ H} ): [k=dfrac{F}{Delta x}=dfrac{1}{0,025}=40text{ H/кг}] Если массу груза увеличить в 3 раза, то есть, (m_2=0,3) кг, то удлинение пружины будет равно: [Delta x=dfrac{F}{k}=dfrac{m_2g}{k}=dfrac{3cdot0,1cdot10text{ H}}{40text{ H/кг}}=0,075text{ м}=7,5text{ см}]
Ответ: 7,5
К системе из кубика массой M = 3 кг и двух пружин приложена постоянная горизонтальная сила F величиной 20 Н (см. рисунок). Между кубиком и опорой трения нет. Система покоится. Жёсткость первой пружины (k_1 = 400 text{ Н/м}). Жёсткость второй пружины (k_2 = 800 text{ Н/м}). Каково удлинение первой пружины? (Ответ дайте в сантиметрах)
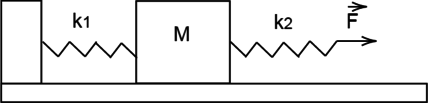
Согласно закону Гука удлинение (Delta x) пружины связано с ее жесткостью k и приложенной к ней силе F выражением (F=kDelta x). На первую пружину действует такая же сила F, что и на вторую, так как трения между кубиком и опорой нет. То, что первая пружина соединена со второй через кубик, здесь не имеет никакого значения, соответственно удлинение первой пружины – это величина, равная: [Delta x=dfrac{F}{k_1}=dfrac{20text{ H}}{400text{ H/м}}=0,05 text{ м}=5 text{ см}]
Ответ: 5
Определите силу, под действием которой пружина жёсткостью 200 Н/см удлинится на 5 мм.
Согласно закону Гука ( F=kDelta x ), где k – жесткость пружины, ( Delta x) – удлинение пружины, получаем: [F=kDelta x=(dfrac{200}{0,01})text{H/м}cdot(5cdot10^{-3})text{м}=100text{ H}]
Ответ: 100
Пружина одним концом прикреплена к неподвижной опоре, к другому концу приложили силу равную 1500 Н, при этом пружина растянулась на 0,2 м. Определите жесткость данной пружины. Ответ дать в Н/м.
После растяжения, пружина покоится и на неё действуют 2 силы направленные в противоположные направления: (F_{text{упр}}) – сила упругости и F – приложенная сила.
Тогда по первому закону Ньютона: [F_{text{упр}}=F] По закону Гука: [F_{text{упр}}=kx] Приравниваем эти формулы: [F=kx] Тогда [k=frac{F}{x}=frac{1500}{0,2}=7500 text{ Н/м}]
Ответ: 7500
К потолку прикреплены одним концом две пружины с одинаковой жесткостью. За другой конец первую пружину растягивают с силой (F_{text{1}}), которая в 2,5 раза больше силы (F_{text{2}}), растягивающей вторую пружину. При этом вторая пружина растянулась на 0,4 м. Насколько растянулась первая пружина? Ответ дать в метрах.
После растяжения обе пружины находятся в покое и на них, кроме данных сил действует сила упругости. Тогда по первому закону Ньютона: [F_{text{упр1}}=F_{text{1}}] [F_{text{упр2}}=F_{text{2}}] где (F_{text{упр1}}) – сила упругости, действующая на первую пружина, (F_{text{упр2}}) – на вторую.
По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [kx_{1}=F_{1}quad(1)] [kx_{2}=F_{text{2}}quad(2)] где (x_{1}) – удлинение первой пружины, (x_{2}) – второй. Разделим (1) на (2), получится: [frac{x_{1}}{x_{2}}=frac{F_{text{1}}}{F_{text{2}}}Rightarrow x_{1}=dfrac{F_{text{1}}x_{2}}{F_{text{2}}}=2,5cdot0,4=1text{ м}]
Ответ: 1
К грузу массой (m) аккуратно подвесили другой груз массой (M), при этом пружина с жесткостью 1200 Н/м удлинилась так, как показано на рисунке. Найдите массу (M). Ускорение свободного падения считать равным 10 м/(c^{2}). Ответ дать в кг.
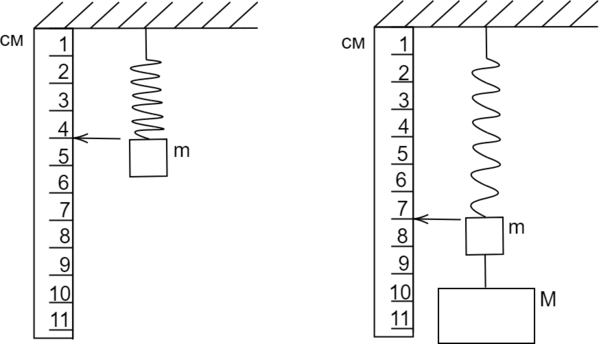
Рассмотрим ситуацию до подвешивания груза: система тел “груз и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg=F_{text{упр}1}] Рассмотрим ситуацию после подвешивания груза: систама тел “2 груза и пружина” покоится, на неё действуют 2 силы, направленные в противоположные стороны: сила тяжести и сила упругости.
Тогда по первому закону Ньютона: [mg+Mg=F_{text{упр2}}] По закону Гука: [F_{text{упр}}=kx] Воспользуемся этим законом в вышенаписанных формулах: [mg=kx_{1}quad(1)] [mg+Mg=kx_{2}quad(2)] Вычтем (1) из (2), получится: [Mg=k(x_{2}-x_{1})Rightarrow M=dfrac{k(x_{2}-x_{1})}{g}=frac{1200cdot0,03}{10}=3,6text{ кг}]
Ответ: 3,6
Источник
- Авторы
- Резюме
- Файлы
Иванов Е.М.
Показано, что работа растяжения пружины A>kxm2 , где k — жесткость пружины, xm — максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
Показано, что работа растяжения пружины A>kxm2 , где k — жесткость пружины, xm — максимальное растяжение. При вычислении работы надо использовать значения x и dx, полученные из решения уравнения движения.
It is shown, that work of a stretching of a spring A>kxm2 , where k — rigidity of a spring, xm — the maximal stretching. At calculation of work it is necessary to use values x and dx, the equations of movement received from the decision.
Рассмотрим спиральную пружину, один конец которой закреплен (рис. 1а), а к другому прикреплен груз массой m. Если пружину растянуть или сжать, то возникает сила F, стремящаяся вернуть тело в положение равновесия. При небольших растяжениях x справедлив закон Гука — сила пропорциональна растяжению пружины: F = -kx. Постоянная k называется коэффициентом упругости, или жесткостью пружины. Знак минус означает, что сила F направлена в сторону, противоположную смещению x, т.е. к положению равновесия x = 0. Геометрически (рис. 1b) , k = tgβ, xm — максимальное (амплитудное) растяжение пружины.
В курсах физики утверждается, что работа при растяжении от x = 0 до xm будет равна
(1)
и эта работа равна потенциальной энергии пружины, растянутой (или сжатой) на величину xm и обладающей жесткостью k. Однако это одно из заблуждений классической механики. Растягивающей силой, равной F = kx, нельзя растянуть пружину даже на долю микрона. Чтобы растянуть пружину, надо приложить растягивающую силу в виде (F1 + k1x ), где F1 >0 (рис. 2а). Уравнение движения (II закон Ньютона) запишем в следующем виде:
(2)
Решение при нулевых начальных условиях (при t = 0, x =0 и V =0) имеет вид
Из решения следует, что если F1 =0, то растяжения пружины не происходит. Амплитудные значения (при x = xm):
Работу вычисляем по формуле , где F = F1 — (k — k1)x, а x и dx определяются из выражений (3) и (4). Работа, совершаемая растягивающей силой
(5)
Работа, совершаемая силой упругости пружины
(6)
Из соотношения (5) следует, что работа, совершаемая растягивающей силой, не зависит от величин F1 и k1 и равна работе
(5а)
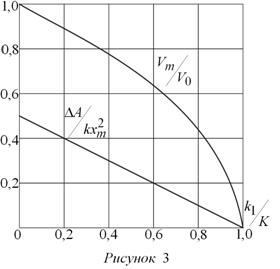
совершаемой постоянной силой F0, при этом работа, совершаемая силой упругости пружины A-0 = -kxm2 разность работ ΔA0 = kxm2 / 2 , конечная скорость при x = xm На рис. 3 даны графики зависимостей Vm / V0 и ΔA = kxm2 от величины отношения K1 / K. ΔA — кинетическая энергия груза.
Рассмотрим случай растягивающей силы FP > F0 (рис.2b) FP = F2 + k2x = F2 — b2x , где b2 = -k2 = tgα. Дифференциальное уравнение движения имеет вид:
(7)
Его решение при нулевых начальных условиях имеет вид:
; (8)
(9)
Амплитудные значения (при x = xm): xm = F2 / mω2; ; .
Работа, совершаемая растягивающей силой
(10)
Работа, совершаемая силой упругости пружины
(11)
Кинетическая энергия груза при x = xm
(12)
На рис. 4 даны графики изменения безразмерных комплексов ΔA / kxm2 и Vm / V0 в зависимости от величины отношения k2 / k.
Рассмотрим третий способ растяжения пружины с грузом (рис. 2с). Прикладываем растягивающую силу Fa >>F0 для растяжения пружины на некоторое расстояние xa, затем сила Fa отключается, а оставшийся отрезок пути, равный xm — xa, груз проходит по инерции, используя запас кинетической энергии Ka, приобретенный в точке xa. Для первого участка пути дифференциальное уравнение имеет вид
(13)
Его решение при нулевых начальных условиях:
; (14)
(15)
Время движения до x = xa
(16)
Работу вычисляем по формуле , где F(x) = Fa — kx, а x и dx определяются выражениями (14) и (15). Работа растяжения на участке до x = x0
(17)
Работа, совершаемая силой упругости пружины на этом же участке
(18)
Кинетическая энергия, приобретенная грузом:
(19)
Для второго участка уравнение движения имеет вид
(20)
Начальные условия для этого уравнения примем в виде: при t = 0 координата x = xa, скорость Va определяется выражением (15) при t = ta. Решение будет иметь вид:
(21)
(21a)
Работа силы упругости пружины на участке от x = xa до xm определится интегралом , где x и dx определяются выражениями (21) и (21а):
(22)
где tm ─ время движения груза от x=xa до x = xm. Условием достижения этой точки является равенство начальной кинетической энергии Ka работе силы упругости пружины A2. Это равенство сводится к трансцендентному уравнению
(23)
где a = kxa2 / 2; b = Ka — a; c = kxaVa / 2ω; φ = ωtm.
Приведем численный пример. Груз массой m = 1 кг, прикрепленный к пружине с жесткостью k = 400 Н/м, растягивается силой F0 = 80 Н на расстояние xm = 0,2. Работа силы растяжения Дж, работа силы упругости пружины Дж, время t = 0,0785 с.
Проведем растяжение силой Fa по схеме, показанной на рис. 2с. Расчет сведем в таблицу 1.
Таблица 1.
Fa [H] | Ka [Дж] | ta [c] | xa [м] | A+ [Дж] | A- [Дж] | tm [c] |
8000 | 8 | 0,0005 | 0,001 | 16 | -8 | 0,078 |
800 | 7 | 0,00468 | 0,00876 | 14,015 | -7,015 | 0,0762 |
200 | 6 | 0,0176 | 0,0309 | 12,19 | -6,19 | 0,0696 |
80 | 3,75 | 0,0377 | 0,054 | 8,088 | -4,338 | 0,0597 |
Таким образом, только в случае растяжения пружины с грузом по схеме, показанной на рис.2с, можно затратить работу на растяжение A+, близкую к потенциальной энергии растянутой пружины П = kxm2 / 2.
Библиографическая ссылка
Иванов Е.М. РАБОТА ДЕФОРМАЦИИ ПРУЖИННОГО МАЯТНИКА // Современные наукоемкие технологии. – 2007. – № 3. – С. 15-19;
URL: https://top-technologies.ru/ru/article/view?id=24676 (дата обращения: 19.10.2020).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Источник
Можно не знать закон Ома и сидеть дома. Но если не знаешь закон Гука – лучше тоже не выходить. Особенно, если идешь на экзамен по физике.
Здесь устраняем пробелы в знаниях и разбираемся, как решать задачи на силу упругости и применение закона Гука. А за полезной рассылкой для студентов добро пожаловать на наш телеграм-канал.
Сила упругости и закон Гука: определения
Сила упругости – сила, препятствующая деформациям и стремящаяся восстановить первоначальные форму и размеры тела.
Примеры действия силы упругости:
- пружины сжимаются и разжимаются в матрасе;
- мокрое белье колышется на натянутой веревке;
- лучник натягивает тетиву, чтобы выпустить стрелу.
Простейшие деформации – деформации растяжения и сжатия.
Закон Гука:
Деформация, возникающая в упругом теле под действием внешней силы, пропорциональна величине этой силы.
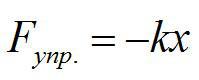
Коэффициент k – жесткость материала.
Есть и другая формулировка закона Гука. Введем понятие относительной деформации «эпсилон» и напряжения материала «сигма»:
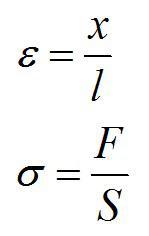
S – площадь поперечного сечения деформируемого тела. Тогда закон Гука запишется так: относительная деформация пропорциональна напряжению.
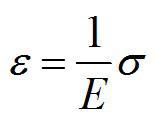
Здесь Е – модуль Юнга, зависящий от свойств материала.
Закон Гука был экспериментально открыт в 1660 году англичанином Робертом Гуком.
Вопросы на силу упругости и закон Гука
Вопрос 1. Какие бывают деформации?
Ответ. Помимо простейших деформаций растяжения и сжатия, бывают сложные деформации кручения и изгиба. Также разделяют обратимые и необратимые деформации.
Вопрос 2. В каких случаях закон Гука справедлив для упругих стержней?
Ответ. Для упругих стержней (в отличие от эластичных тел) закон Гука можно применять при малых деформациях, когда величина эпсилон не превышает 1%. При больших деформациях возникают явления текучести и необратимого разрушения материала.
Вопрос 3. Как направлена сила упругости?
Ответ. Сила упругости направлена в сторону, противоположную направлению перемещения частиц тела при деформации.
Вопрос 4. Какую природу имеет сила упругости?
Ответ. Сила упругости, как и сила трения – электромагнитная сила. Она возникает вследствие взаимодействия между частицами деформируемого тела.
Вопрос 5. От чего зависит коэффициент жесткости k? Модуль Юнга E?
Ответ. Коэффициент жесткости зависит от материала тела, а также его формы и размеров. Модуль Юнга зависит только от свойств материала тела.
Задачи на силу упругости и закон Гука с решениями
Кстати! Для наших читателей действует скидка 10% на любой вид работы.
Задача №1. Расчет силы упругости
Условие
Один конец проволоки жестко закреплен. С какой силой нужно тянуть за второй конец, чтобы растянуть проволоку на 5 мм? Жесткость проволоки известна и равна 2*10^6 Н/м2.
Решение
Запишем закон Гука:
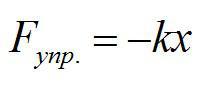
По третьему закону Ньютона:
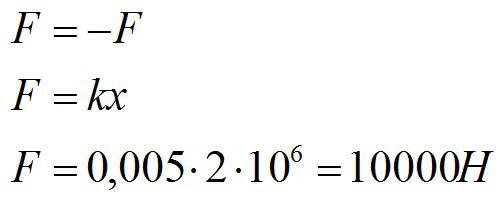
Ответ: 10 кН.
Задача №2. Нахождение жесткости пружины
Условие
Пружину, жесткость которой 100 Н/м, разрезали на две части. Чему равна жесткость каждой пружины?
Решение
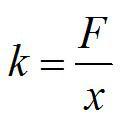
По определению, жесткость обратно-пропорциональна длине. При одинаковой силе F неразрезанная пружина растянется на х, а разрезанная – на x1=x/2.
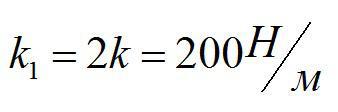
Ответ: 200 Н/м
При растяжении пружины в ее витках возникают сложные деформации кручения и изгиба, однако мы не учитываем их при решении задач.
Задача №3. Нахождение ускорения тела
Условие
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Решение
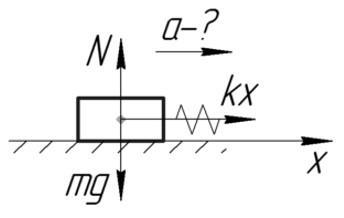
За силу, которая приложена к телу и заставляет его двигаться, можно принять силу упругости. По второму закону Ньютона и по закону Гука:
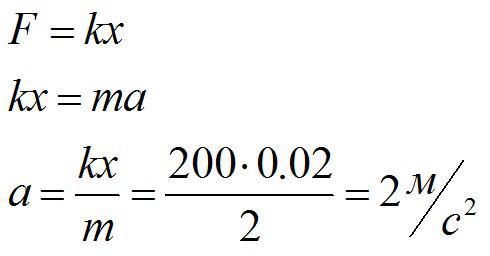
Ответ: 2 м/с^2.
Задача №4. Нахождение жесткости пружины по графику
Условие
На графике изображена зависимость модуля силы упругости от удлинения пружины. Найти жесткость пружины.
Решение
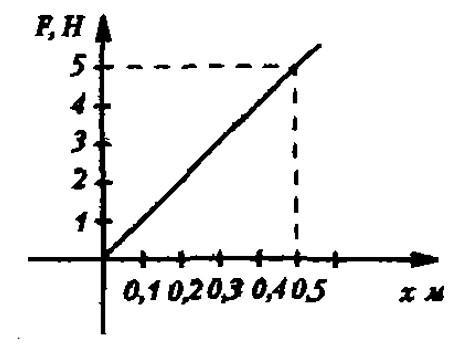
Вспоминаем, что жесткость равна отношению силы и удлинения. Представленная зависимость – линейная. В любой точке прямой отношение ординаты F и абсциссы х дает результат 10 Н/м.
Ответ: k=10 Н/м.
Задача №5. Определение энергии деформации
Условие
Для сжатия пружины на х1=2 см надо приложить силу 10 Н. Определить энергию упругой деформации пружины при сжатии на х2=4 см из недеформированного состояния.
Решение
Энергия сжатой пружины равна:
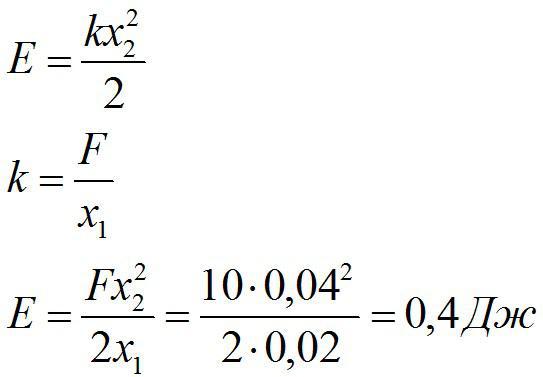
Ответ: 0,4 Дж.
Нужна помощь в решении задач? Обращайтесь за ней в профессиональный студенческий сервис.
Автор
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Источник
